 |
ادرس خط الأعداد التالي:
 |
ـ كم بُعد العدد الصحيح ( +3 ) عن النقطة المرجعية التي تمثل الصفر على خط الأعداد ؟؟
 |
ـ وكم بُعد العدد الصحيح ( -3 ) عن النقطة المرجعية التي تمثل الصفر عن خط الأعداد ؟؟
 |
ـ لاحظ أنّ العدد ( -3 ) هو النظير الجمعي للعدد ( +3 ) ، وتقول كذلك العدد ( +3 )هو النظير الجمعي للعدد ( -3 ) .
طبعاً أنت تعرف أن العدد الصحيح ونظيره الجمعي يكونان على بُعدين متساويين من النقطة المرجعية التي تمثل الصفر على خط الأعداد .
تذكر :
بُعد النقطة التي تمثل العدد الصحيح على خط الأعداد عن النقطة المرجعية هو القيمة المطلقة لذلك العدد . بُعد العدد الصحيح ( +3 ) عن النقطة المرجعية هو ( 3 ) وحدات ، وبُعد العدد الصحيح ( -3 ) عن النقطة المرجعية هو( +3 ) وحدات .
أي أن : |+3 | = | -3 |
 |
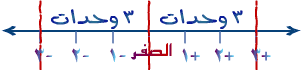لاحظ أن : 3 وحدات = | +3 |
= | +3 ـ صفر | أو | صفر ـ (+3) |
وكذلك 3 وحدات = | ـ3 |
= | (ـ3) ـ صفر | أو | صفر ـ (ـ3) |
في خط الأعداد التالي إحداثي النقطة أ = س1 هو ( +1 ) وإحداثي النقطة ب = س2 هو ( +4 )، ويُمكننا القول أن إحداثي النقطة المرجعية على خط الأعداد م = س0 هو الصفر .
مثل 1 :
 |
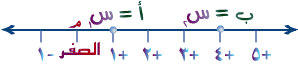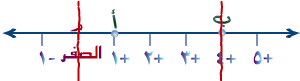 | الآن ........ (1) كم بُعد النقطة ب عن النقطة المرجعية م ؟؟ |
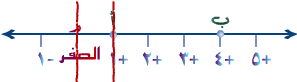 | (2) وكم بُعد النقطة أ عن النقطة المرجعية م ؟؟ |
حسناً ... ! (3) كم بُعد النقطة ب عن النقطة أ ؟؟ (4) وكم بعد النقطة أ عن النقطة ب ؟؟ |
| احداثي النقطة ب ـ احداثي النقطة م| | 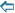 | بُعد النقطة ب عن النقطة المرجعية هو |
= |س2 ـ س0| | ||
 | ||
= |س0 ـ س2| | احداثي النقطة م ـ احداثي النقطة ب| | 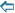| وكذلك نقول بُعد النقطة ب عن النقطة المرجعية |
 | ||
بُعد النقطة ب عن النقطة أ هو
 |
|
مثل 2 :
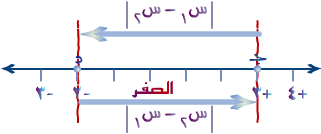
على خط الأعداد التالي ، إذا كان إحداثي النقطة جـ = س1 هو ( +3 )، وإحداثي النقطة د = س2 هو ( ـ2 )،
فكم البُعد بين النقطتين ( جـ ) ، ( د ) ؟؟؟؟؟؟
 |
| إحداثي النقطة جـ ـ إحداثي النقطة د | أو | إحداثي د ـ إحداثي جـ |
وكذلك.... | س2 ـ س1 | = | ( -2 ) ـ ( +3 ) | = | ـ 5 | = +5 وحدات | وبالتالي : | س1 ـ س2 | = | ( +3 ) ـ ( -2 ) | = 5 وحدات |
 |
ماذا نستنتج ...
 المسافة بين أي نقطتين على خط الأعداد تساوي :| إحداثي النقطة الأولى - إحداثي النقطة الثانية | أو نقول | إحداثي النقطة الثانية - إحداثي النقطة الأولى | |
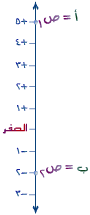 | لندرس الآن المسافة بين نقطتين في خط الأعداد المرسوم بوضع عمودي. في الرسم المجاورذا كان إحداثي النقطة ( أ ) = ص1 هو ( +5 ) ، وإحداثي النقطة ( ب ) = ص2 هو ( -2 ) فإن : |
بُعد النقطة ( أ ) عن النقطة المرجعية م = ص0 (الصفر) هو القيمة المطلقة لإحداثي النقطة أ = | +5 | = 5 وحدات لاحظ أن 5 وحدات = | +5 | = | ص1 – ص0 | أو | ص0 – ص1 | = | ( +5 ) – ( 0 ) | أو | ( 0 ) ـ ( -5 ) | |
وكذلك فإن بُعد النقطة ( ب ) عن النقطة المرجعية هو القيمة المطلقة لإحداثي النقطة ( ب ) | -2 | لاحظ أن ..... | -2 | = 2 وحدة = | ص2 – ص0 | أو | ص0 – ص2 | = | ( -2 ) – ( 0 ) | أو | ( 0 ) – ( -2 ) | = | -2 | أو | +2 | = 2 وحدة |
الآن ما هي المسافة بين النقطتين ( أ ) ، ( ب ) ؟؟ نقول البُعد بين ( أ ) ، ( ب ) هو | إحداثي أ – إحداثي ب | أو نقول | إحداثي ب – إحداثي أ | | ص1 – ص2 | | ص2 – ص1 | | ( +5 ) – ( -2 ) | | ( -2 ) – ( +5 ) | | 7 | | -7 | = 7 وحدات |
0 التعليقات:
إرسال تعليق