Copyright © 2001 - 2010 SchoolArabia. All right
الهدف :
أن يتعرف الدارس إلى كيفية الكتابة الرياضية لمجموعةٍ ما بذكر عناصرها .
أن يتعرف الدارس إلى كيفية الكتابة الرياضية لمجموعةٍ ما بذكر عناصرها .
الخبرات السابقة :
مفهوم المجموعة , العنصر , إنتماء أو عدم إنتماء العنصر إلى مجموعة ما (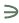 ,
,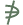 )
)
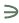 ,
,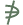 )
) تمهيد :
1) نستخدم اشارة الحاصرتين { } لكتابة عناصر مجموعة ما داخلهما .
مثل :
مجموعة الفصول الأربعة هي : الصيف ، الشتاء ، الربيع ، الخريف
وبالتالي نكتب مجموعة الفصول الأربعة = } الصيف ، الشتاء ، الربيع ، الخريف {
2) عندما نكتب عناصر مجموعة ما داخل اشارة الحاصرتين { } لاحظ أننا نصنع الفاصلة ( ، )
بين كل عنصرٍ وآخر .
بين كل عنصرٍ وآخر .
مجموعة الأعداد الزوجية المحصورة بين العدد (1) و العدد (11) = { 2 , 4 , 6 , 8 , 10}
3) إذا كانت س هي مجموعة الفقاريات التي تضم :
(الأسماك ، الزواحف ، الطيور ، البرمائيات ، الثدييات ) فإننا نستطيع التعبير رياضياً عن هذه المجموعة كالتالي
س = } الأسماك ، الزواحف ، الطيور ، البرمائيات ، الثدييات {
وكذلك
س = } الثدييات ، الطيور ، البرمائيات ، الزواحف ، الأسماك {
وكذلك
س = } الزواحف ، البرمائيات ، الثدييات ، الأسماك ، الطيور {
ماذا تُلاحظ !!
نحن نذكر عناصر المجموعة داخل الحاصرتين وبأي ترتيب كان ، إذن :
s reserved الحقوق القانونية و حقوق الملكية الفكرية محفوظة للمدرسة العربية
كتابة المجموعة بذكر الصفة المميزة
الهدف : أن يتعرف الدارس إلى كيفية الكتابة الرياضية لمجموعة ما بذكر الصفة المميزة لعناصرها.
الإجراءات والأنشطة :
أولاً :
الصفة المميزة | المجموعة | ||
كل عنصر هو فصل من فصول السنة | س = } الصيف ، الربيع ، الشتاء ، الخريف { | 1. | |
كل عنصر هو عدد زوجي يقع بين 1 ، 9 | ع = { 2 ، 4 ، 6 ، 8 } | 2. | |
كل عنصر هو عدد فردي يقع بين 10 ، 20 | ل = { 11 ، 13 ، 15 ، 17 ، 19 } | 3. | |
كل عنصر هو يوم من أيام الأسبوع | و = } السبت ، الأحد ، الاثنين ، الثلاثاء ، الاربعاء ، الخميس والجمعة{ | 4. | |
يمكننا التعبير عن مجموعة ما ، بكتابة الصفة المميزة بدلاً من ذكر وكتابة عناصرها
مثل1 :
المجموعة الأولى = } س : س فصل من فصول السنة {
وتُقرأ مجموعة فصول السنة ( س ) حيث س فصل من فصول السنة .
المجموعة الثانية = } ع : ع عدد زوجي يقع بين 1 ، 9 {
وتُقرأ مجموعة الأعداد الزوجية ( ع ) ، حيث ع عدد زوجي يقع بين 1 ، 9 .
المجموعة الثالثة : ص = } ل : ل عدد فردي يقع بين 10 ، 20 {
وتُقرأ ص مجموعة الأعداد الفردية ( ل ) حيث ل عدد فردي يقع بين 10 ، 20 .
المجموعة الرابعة : س = } و : و يوم من أيام الأسبوع {
وتقرأ س مجموعة أيام الاسبوع ( و ) حيث و يوم من أيام الأسبوع .
مثل2 :
كيف تقرأ التالي : ص = } س : س عدد فردي يقع بين 2 ، 10 {
نقول ص مجموعة الأعداد الفردية س حيث س عدد فردي يقع بين 2 ، 10
ونستطيع القول :
ص مجموعة الأعداد س حيث س عدد فردي أكبر من 2 وأصغر من 10
ص مجموعة الأعداد س حيث س عدد فردي أكبر من 2 وأصغر من 10
}س : س .... { تُقرأ مجموعة س حيث س .....
مثل 3 :
1) المجموعة ص = } س : س عدد يقبل القسمة على 5 ، ويقع بين 1 ، 101 } تكتب أيضاً على الصورة
ص = { 5 ، 10 ، 15 ، 20 ، 25 ، 30 ، ... ، 100}
وهذه النقط ، ... ، تعني أننا نقصد استمرار كتابة العناصر الأخرى حتى نصل إلى العدد الأخير 100 . |
2) المجموعة ع = } ل : ل عدد زوجي أكبر من 1 {
ع = { 2 ، 4 ، 6 ، 8 ، ...}
النقاط .... في هذه المجموعة تشير إلى استمرارية كتابة العناصر على نفس المنوال دون انتهاء . |
ما هو أكبر عدد زوجي تعرفه !!هل تعرف ما هو أكبر عدد زوجي !!
عدد عناصر المجموعة
الهدف : أن يتعرف الدارس إلى العلاقة بين عناصر مجموعة ما وعدد هذه العناصر .
الإجراءات والأنشطة :
الإجراءات والأنشطة :
1) يتكون العدد 635 من ثلاثة أرقام مميزة هي 5 ، 3 ، 6 .
نقول س = { 5 ، 3 ، 6 } وتُقرأ
(س) مجموعة أرقام العدد 635
ـ كم عدد عناصر المجموعة س ؟؟ 3 عناصر مميزة (مختلفة) .
2) تتكون كلمة فلسطين من ستة أحرف مميزة هي ف ، ل ، س ، ط ، ي ، ن
نقول ص = } ف ، ل ، س ، ط ، ي ، ن { وتُقرأ
(ص) مجموعة أحرف كلمة فلسطين
ـ كم عدد عناصر المجموعة ص ؟؟ 6 عناصر مميزة .
3) يتكون العدد 212 من ثلاثة أرقام : هي 2 ، 1 ، 2
وهو يتكون من رقمين مميزين هما 2 ، 1
وتتكون كلمة جنين من أربعة أحرف ! هي ج ، ن ، ي ، ن
ولكن هذه الكلمة تتكون من ثلاثة (3) أحرف مميزة (مختلفة) هي ج ، ن ، ي
تُرى كيف ستكتب المجموعة المعبرة عن أرقام العدد 212 بذكر عناصرها !
س = { 2 , 1 , 2 } أو س = { 1 , 2 } س = { 1 , 2 ( مكرر مرتان )}
المجموعة المعبرة عن أحرف كلمة جنين
ص =} ه(1)ج ، (1) ي ، (2) ن { | أو | ص = } ج ، ي ، ن { | أو | ص = } ج ، ي ، ن ، ن { |
هل تُلاحظ فرقاً أو اختلافاً في هذه الحالات !!
عدد عناصر المجموعة
بشكل عام نحن لا نكرر كتابة عناصر المجموعة داخل الاقواس حيث نكتفي بكتابة العناصر المميزة ، وذلك للإختصار وعدم الاطالة .
ولكن يلزمنا في بعض الأحيان أن نتعرف إلى عدد العناصر الكلي لمجموعة ما ، وعندها يُمكنناكتابة كافة عناصر المجموعة المميزة مع كتابة تكرار كل واحد منها .
ولكن يلزمنا في بعض الأحيان أن نتعرف إلى عدد العناصر الكلي لمجموعة ما ، وعندها يُمكنناكتابة كافة عناصر المجموعة المميزة مع كتابة تكرار كل واحد منها .
لاحظ أن ص = } ج ، ي ، ن { تُعبر عن مجموعة أحرف كلمة جنين .
وكذلك ص = } ج ، ي ، ن ، ن { تعبر عن مجموعة أحرف كلمة جنين .
وكذلك ص = } ج ، ي ، ن (مكرر مرتان ) { تُعبر عن مجموعة أحرف كلمة جنين .
وبالمثل :
س = { 1 , 2 } تُعبر عن مجموعة أرقام العدد 212 .
س = { 1 , 2 , 2 } تُعبر عن مجموعة أرقام العدد 212 .
س = { 2 مكرر مرتان , 1 } تُعبر عن مجموعة العدد 212
4) يتكون العدد 5755 من أربعة ارقام ! هي 5 ، 5 ، 7 ، 5 وهو يتكون من رقمين مميزين 5 ، 7
نقول ع = { 5 , 7 } وهنا عدد عناصر المجموعة يدلنا على عدد الأرقام المميزة في مجموعة أرقام العدد 5755 .
ونقول : ع = { 5 ( مكرر ثلاث مرات ) , 7 }
ع = { 5 , 7 , 5 , 5 }
ع = { 5 , 7 , 5 , 5 }
وعدد العناصر هنا يدُّلنا على العدد الكلي لارقام ( عناصر ) العدد 5755 .
وبالمثل :
إذا كانت س هي مجموعة أحرف كلمة رياضيات , نقول :
س = } ر ، أ ، ي ، ض ، ت {
وعدد العناصر هنا يدُّلنا على عدد الأحرف المميزة في كلمة رياضيات .
ونقول : س = } ر ، ي ، أ ، ض ، ي ، أ ، ت {
وعدد العناصر هنا يدَّلنا على العدد الكلي لاحرف كلمة رياضيات .
سؤال : عبّر عن كل مجموعة مما يأتي بطريقة ذكر العناصر :
س = مجموعة أيام الأسبوع
ص = مجموعة أرقام العدد 2562
ع = مجموعة أسماء أفراد أسرتك .
المجموعة الجزئية
الهدف : أن يتعرف الدارس إلى مفهوم المجموعة الجزئية وعلاقتها بالمجموعة الرئيسة .
الاجراءات والأنشطة :
لنأخذ المجموعة س التي تمثل أرقام العدد 8624
س = { 4 , 2 , 6 , 8 }
يمكننا تكوين مجموعة أو مجموعات جزئية من هذه المجموعة الرئيسة بأخذ عنصر أو أكثر منها وكتابتها ضمن مجموعة جديدة .
ع = { 6 , 8 , 2} | ص = { 4 } |
د = { 6 , 2 , 4 } ... وهكذا | ل = {4 , 6 } |
ماذا تُلاحظ هنا : كل عناصر ع تنتمي إلى س
كل عناصر ل تنتمي إلى س
كل عناصر د تنتمي إلى س
كل عناصر ص تنتمي إلى س
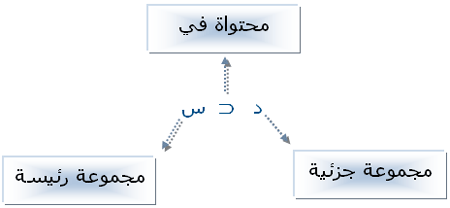
نقول هنا: ع مجموعة جزئية من س أو نقول ع محتواة في س
نعبر عن هذه الجمل بالصورة الرياضية التالية ع ة س
نقول: ل محتواة في س
ل ة ... تُقرأ ل محتواه في ... | ل ة س |
أو ل مجموعة جزئية من .....
ونقول: المجموعة ص مجموعة جزئية من المجموعة الكلية س
ص ة ... تُقرأ ص محتواة في ....... | ص ة س |
أو ص مجموعة جزئية من .....
 |
المجموعة الجزئية
الرمز 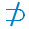 : يُقرأ غير محتواة في ويُقرأ أيضاً مجموعة غير جزئية من : يُقرأ غير محتواة في ويُقرأ أيضاً مجموعة غير جزئية من |
مثل : إذا كانت س = } أحمر ، أخضر ، أصفر {
وكانت ص = } أزرق ، بني {
لاحظ هنا أنَّ عناصر ص غير محتواة في س
نقول : ص
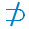 س
سص غير محتواة في س أو ص مجموعة غير جزئية من س
مثل : إذا كانت ع = } أ ، ب ، ت ، ث {
م = } أ ، ب ، ل {
العنصر ل 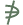 ع ع | العنصر ل 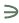 م م |
العنصر ت 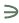 ع ع | العنصر ت 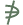 م م |
ع 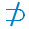 م م | وكذلك | م 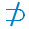 ع ع |
ع مجموعة غير جزئية من م | م غير محتواة في ع |
مثل : إذا كانت س = { 2 ، 4 ، 6 } ، 6
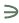 س
س ص = { 2 ، 4 } , 6 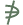 ص
ص
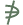 ص
صماذا تستنتج !؟س
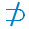 ص ، س غير محتواة في ص
ص ، س غير محتواة في صولكن :
كل عناصر ص محتواة في س
ص ة س ، ص محتواة في س
ص ة س ، ص محتواة في س
ص مجموعة جزئية من س
نقول أن المجموعة ص مجموعة جزئية من المجموعة س إذا وفقط كان كل عنصر من عناصر المجموعة ص ينتمي إلى المجموعة س . |
سؤال : إذا كانت س = { 2 ، 3 ، 5 ، 7 ، 9}
عين أي المجموعات الآتية مجموعة جزئية من س وأيها ليست جزئية من س مع ذكر السبب ؟؟
عين أي المجموعات الآتية مجموعة جزئية من س وأيها ليست جزئية من س مع ذكر السبب ؟؟
ب = { 9 } | أ = { 3 , 1 } |
د = { 2 ، 3 ، 6} | ج = { 2 ، 5 ، 7} |
المجموعات المتكافئة ( التساوي )
الهدف : أن يتعرف الدارس إلى مفهوم المجموعة المتكافئة .
الإجراءات والأنشطة :
الإجراءات والأنشطة :
مثل1 :
ما العلاقة بين س ، ص إذا كانت س مجموعة أحرف كلمة عنب ، و ص مجموعة أحرف نَبع .
ما العلاقة بين س ، ص إذا كانت س مجموعة أحرف كلمة عنب ، و ص مجموعة أحرف نَبع .
س = } ع ، ن ، ب { ، ص = } ن ، ب ، ع {
ماذا تُلاحظ :
أولاً :
2) كل عنصر في ص ينتمي إلى س | 1) كل عنصر في س ينتمي إلى ص |
أي أن كلاً من س و ص تحتويان نفس العناصر | |
ثانياً :
2) المجموعة ص محتواة في المجموعة س | 1) المجموعة س محتواة في المجموعة ص |
ص ة س | س ة ص |
ماذا تستنج !؟
س = ص إذا وفقط كانت س ة ص وكذلك ص ة س.
س = ص إذا وفقط كانت س ة ص وكذلك ص ة س.
مثل2 :
ما العلاقة بين س ، ص إذا كانت
س مجموعة أحرف كلمة دمار ، و ص مجموعة أحرف كلمة مارد
س = } د ، م ، ا ، ر { ، ص } م ، ا ، ر ، د {
هل تذَّكر أن ترتيب العناصر داخل المجموعة لا يغير المجموعة !!
لاحظ هنا : كل عناصر س محتواة في ص
(كل عنصر في س ينتمي إلى ص)
س ة ص
وكذلك : كل عناصر ص محتواة في س
وكذلك : كل عناصر ص محتواة في س
(كل عنصر في ص ينتمي إلى س )
ص ة س
س ة ص ، ص ة س
نقول هنا : س = ص أي أن س ، ص تتكونا من العناصر نفسها .
مثل3 :
إذا كانت س هي مجموع أرقام العدد 959442 ، و ص هي مجموعة أرقام العدد 2495
إذا كانت س هي مجموع أرقام العدد 959442 ، و ص هي مجموعة أرقام العدد 2495
فما هي العلاقة بين س ، ص؟
الحل :
س = {2 ، 4 ، 9 ، 5 }
ص = { 5 ، 9 ، 4 ، 2}
بما أن عناصر س المميزة هي نفس عناصر ص المميزة .إذن: س ة ص
ص ة س
ص ة س
وبالتالي: س = ص
المجموعة الخالية
الهدف : أن يتعرف الدارس إلى مفهوم المجموعة الخالية ، ورمزها { } أو f
الإجراءات والأنشطة :
أولاً :
أولاً :
7 ـ 7 = صفر , 7 ـ صفر = 7 , 4 ، 3 ، 2 ، 1 ، ؟؟
ثانياً :
كم عدد عناصر المجموعة ص = } أصفر ، أخضر ، أحمر {
وكم عدد عناصر المجموعة س = } أصفر ، أخضر{
وكم عدد عناصر المجموعة ع = } أصفر {
والآن : كم عدد عناصر المجموعة خ = { }
حسناً : واضح أن المجموعة خ تخلو من العناصر .
ونقول : خ = { } ، f أي مجموعة دون عناصر .
نسمي المجموعة التي تخلو من العناصر المجموعة الخالية .
4) إذا أردت أن تكتب المجموعة س لتمثل الطلبة الذين تزيد أعمارهم عن 70 سنة في صفك ! ماذا تفعل ؟؟
س = { }
أي أن س مجموعة تخلو من أي عنصر
5) وماذا عن ص إذا كانت هي مجموعة الأطفال الرضع الذين يزيد وزنهم على 100 كغم ؟؟
ص = f
أي أن ص مجموعة تخلو من أي عنصر
الحرف f يُلفظ "فاي" |
نُسمي المجموعة التي تخلو من العناصر المجموعة الخالية أو الفارغة ويرمز لها بالحرفf
المجموعة الخالية
6) إذا كانت ع هي مجموعة الألوان أحمر ، أصفر ، أزرق ، أبيض .
أ) فما هي مجموعة الالوان الجزئية ص التي تنتهي بالحرف ض .
ب) وما هي مجموعة الالوان الجزئية س التي تنتهي بالحرف ر.
ج) وما هي مجموعة الالوان الجزئية خ التي تنتهي بالحرف د.
د) وما هي مجموعة الالوان الجزئية ف التي تبدأ بالحرف ب .
لنرى معاً :
نكتب المجموعة ع كالتالي : ع = } أحمر ، أصفر ، أزرق ، أبيض {
أ) ص = } أبيض {
ب) س = } أحمر ، أصفر {
ج) خ = { } مجموعة فارغة تخلو من العناصر
د) ف = f مجموعة فارغة تخلو من العناصر
سؤال : عين المجموعة الخالية فيما يأتي :
ـ مجموعة الأعداد الأولية المحصورة بين 5 ، 13.
ـ مجموعة الأعداد الطبيعية المحصورة بين 10 ، 11 .
ـ مجموعة الدول العربية في قارة أوروبا .
ـ مجموعة الأعداد الزوجية المحصورة بين 1 ، 11 .
ـ س = { صفر }
أولاً : أدرس المجموعات التالية : أ = مجموعة مضاعفات العدد 5 .
ب = مجموعة الكسور .
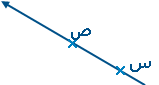 |  | = مجموعة نقاط الشعاع |  |
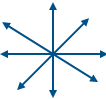 | ن مجموعة المستقيمات التي تمر بالنقطة م |
هل تستطيع حصر عدد مضاعفات العدد 5 ؟
وهل تستطيع حصر عدد المستقيمات التي تمر بالنقطة م ؟
وهل تستطيع حصر عدد المستقيمات التي تمر بالنقطة م ؟
ماذا تلاحظ ؟؟
يستحيل تحديد عدد عناصر أي من المجموعات هذه .
نُسمي المجموعة التي لا يُمكن تحديد ( تعيين ) عدد عناصرها مجموعة غيرُ منتهية |
1) ص = { 1 , 3 , 5 , ...... }
نقول عن المجموعة ص أنها مجموعة محصورة من الأسفل .
نقول عن المجموعة ص أنها مجموعة محصورة من الأسفل .
ص = أ : أ الأعداد الفردية £ 1
لاحظ هنا أن المجموعة ص غير محصورة من أعلى .
لاحظ هنا أن المجموعة ص غير محصورة من أعلى .
2) ع = { 2 , 1 , 0 , ـ1 , ـ 2 , ........ }
نقول عن المجموعة ع أنها مجموعة محصورة من الأعلى .
نقول عن المجموعة ع أنها مجموعة محصورة من الأعلى .
ونلاحظ أنها غير محصورة من أسفل .
سؤال : حدد المجموعات غير المنتهية من بين المجموعات الآتية وعبر عن كل مجموعة منها بطريقة ذكر العناصر .
مجموعة أشهر السنة الهجرية . مجموعة مضاعفات العدد 2 .
مجموعة الاعداد الطبيعية . مجموعة الأعداد التي تقبل القسمة على 3.
مجموعة أشهر السنة الهجرية . مجموعة مضاعفات العدد 2 .
مجموعة الاعداد الطبيعية . مجموعة الأعداد التي تقبل القسمة على 3.
ثانياً : أدرس المجموعات التالية :س = { 2 ، 4 ، 6 ، 8}
ص = مجموعة أيام الأسبوع .
ص = مجموعة أيام الأسبوع .
ع = مجموعة أحرف كلمة سمسم .
ل = مجموعة طلبة صفك .
م = مجموعة مدن العراق .
م = مجموعة مدن العراق .
ـ هل تستطيع تحديد عناصر المجموعة س .
ـ عبر عن المجموعة ص بطريقة ذكر العناصر .
ـ هل يمكنك معرفة وتحديد عدد عناصر المجموعة ل .
ـ هل يمكنك معرفة وتحديد عدد عناصر المجموعة ل .
ـ كيف يمكنك الحصور على المعلومات اللازمة لذكر عناصر المجموعة م .
ماذا تلاحظ ؟!المجموعات س ، ص ، ع ، ل ، م هي مجموعات يمكننا تحديد ومعرفة عدد عناصرها .
ماذا تلاحظ ؟!المجموعات س ، ص ، ع ، ل ، م هي مجموعات يمكننا تحديد ومعرفة عدد عناصرها .
المجموعة التي يمكن تحديد ( تعيين ) عدد عناصرها تُسمى مجموعة منتهية . |
1) س = { 2 , 4 , 6 , .... , 98 , 100 }
نقول عن المجموعة س أنها مجموعة منتهية , فهي محصورة من الأسفل ومحصورة أيضاً من الأعلى .
نقول عن المجموعة س أنها مجموعة منتهية , فهي محصورة من الأسفل ومحصورة أيضاً من الأعلى .
س = أ : أ الأعداد الزوجية المحصورة بين 1 وَ 101 .
سؤال :حدد المجموعات المنتهية من المجموعات الآتية وعبر عن كل مجموعة بطريقة ذكر العناصر .
مجموعة المربعات . مجموعة أشهر السنة الميلادية .
مجموعة مضاعفات العدد 4 . مجموعة عوامل العدد 5.
مجموعة الأعداد الطبيعية الزوجية المحصورة بين 5 ، 15 .
قطعة مستقيمة والنقطتان س ، ص تقعان خارج | 1) في الشكل التالي ، |
هذه القطعة المستقيمة .
نقول :
الآن ، أدرس الشكل ، مع ملاحظة أنَّ القطعة المستقيمة |
نقول :
. |  | ، |  | 2) الشكل التالي يُمثل قطعتين مستقيمتين هما |
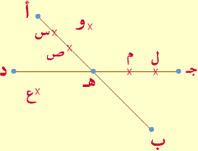 | القطعة المستقيمة، بشكل عام، تتكون من مجموعة من النقاط، وفي المثال هنا نرى أن النقاط أ، س،
بينما النقاط ل ، م ، هـ ، د هي من مجموعة نقاط
|
 النقاط س ، ص ، تنتمي إلى القطعة
النقاط س ، ص ، تنتمي إلى القطعة  .
.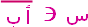 ،
، 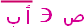
 النقاط ل ، م تنتمي إلى القطعة
النقاط ل ، م تنتمي إلى القطعة  .
.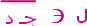 ،
، 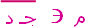
 |  النقطة هـ كما هو موضح بالشكل تنتمي إلى النقطة هـ كما هو موضح بالشكل تنتمي إلى  وكذلك تنتمي إلى وكذلك تنتمي إلى  . .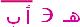 ، ، 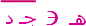 |
 النقطة ع لا تنتمي إلى القطعة
النقطة ع لا تنتمي إلى القطعة  ، وكذلك النقطة ع لا تنتمي إلى القطعة
، وكذلك النقطة ع لا تنتمي إلى القطعة  .
. 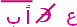 ،
، 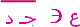
 أدرس الشكل جيِّداً ، وحاوِل الإجابة عن الأسئلة التالية :
أدرس الشكل جيِّداً ، وحاوِل الإجابة عن الأسئلة التالية : |  هل هنالك نقاط أخرى غير (هـ) تنتمي إلى كلٍّ من هل هنالك نقاط أخرى غير (هـ) تنتمي إلى كلٍّ من  ، ،  ؟ ؟ كيف نُعبِّر عن انتماء النقطة (هـ) إلى كلٍّ من كيف نُعبِّر عن انتماء النقطة (هـ) إلى كلٍّ من  ، ،  ؟ ؟ كم عنصراً في المجموعة كم عنصراً في المجموعة  تقاطع تقاطع  ؟ ؟ |
3) تأمل الشكل التالي جيِّداً ، ثم حدِّد صحة أو خطأ العبارات التالية :
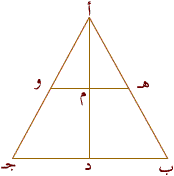 | 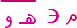 | |
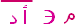 | ||
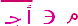 | ||
 | 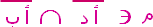 | |
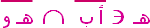 | ||
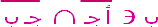 | ||
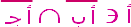 |
4) أدرس رسم المستطيل أ ب جـ د ثم أجب عن الأسئلة التالية :
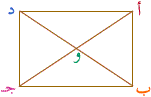
و 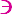 أ جـ أ جـ | |
أ 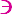 أ د أ د |
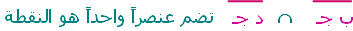 | |
 |
والآن ...
 | ماذا عن تقاطع  ، ،  ؟؟ ؟؟ماذا عن تقاطع  ، ،  ؟؟ ؟؟ |
درست سابقاً أن :
 زوايا المستطيل الأربع زوايا المستطيل الأربع |
 كل ضلعين متقابلين في المستطيل متساويان في الطول و كل ضلعين متقابلين في المستطيل متساويان في الطول و |
كيف نُعرِّف ، ونحدد توازي مستقيمين ؟
درست سابقاً أننا عند رسم مستقيمين ، يتعين أحد أمرين :
 يتقاطع المستقيمان ، وتوجد نقطة تنتمي إلى كلٍّ منهما .
يتقاطع المستقيمان ، وتوجد نقطة تنتمي إلى كلٍّ منهما .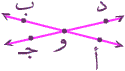
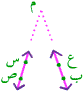
 لا يتقاطع المستقيمان ، كما في الشكل التالي
لا يتقاطع المستقيمان ، كما في الشكل التالي
نرمز لعلامة التوازي بالرمز ( // ) وهكذا نقول جـ د // أ ب .
لاحظ أن العبارة " لا يتقاطع المستقيمان " تدل على عدم وجود نقطة تنتمي إلى كلٍّ منهما ، أي أن جـ د أ ب هو مجموعة خالية ورمزها (
أ ب هو مجموعة خالية ورمزها (  ) ماذا تستنتج ؟؟
) ماذا تستنتج ؟؟
 أ ب هو مجموعة خالية ورمزها (
أ ب هو مجموعة خالية ورمزها (  ) ماذا تستنتج ؟؟
) ماذا تستنتج ؟؟يقال لمستقيمين أنهما متوازيان إذا كان تقاطعهما مجموعة خالية . |


0 التعليقات:
إرسال تعليق